Fungsi Kuadrat

Fungsi kuadrat atau yang dikenal juga sebagai fungsi polinom adalah fungsi dengan pangkat peubah tertingginya adalah 2.

Pada umumnya, bentuk umum dari fungsi kuadrat adalah f(x)=ax2+bx+c atau y=ax2+bx+c.

Suatu fungsi selalu berkaitan dengan grafik fungsi. Begitu juga dengan yang ada pada fungsi kuadrat.

Grafik fungsi kuadrat memiliki bentuk seperti parabola. Untuk menggambar grafik fungsi kuadrat harus ditentukan titik potong dengan sumbu koordinat dan juga titik ekstrim.

Adapun sebutan lain untuk titik ekstrim yaitu titik puncak atau titik maksimum atau minimum. Dan sekarang kita membasa masing-masing dari titik tersebut. Simak pembahasannya berikut ini.

Titik Potong dengan Sumbu Koordinat

Titik potong dengan sumbu X didapatkan dengan cara menentukan nilai peubah x pada fungsi kuadrat. Apabila nilai peubah y sama dengan nol, sehingga akan didapatkan titik potong (x1,0) dan (x2,0).

Yang mana x1 dan x2 adalah akar-akar persamaan kuadrat.

Namun perlu kalian ingat bahwasannya berbagai akar persamaan kuadrat tergantung dari diskriminannya.

Apabila diskriminannya sama dengan nol maka akan didapatkan hanya satu akar dan ini berarti hanya ada satu titik potong dengan sumbu X.

Jika nilai diskriminannya kurang dari nol persamaan kuadrat tersebut tidak mempunyai akar real yang berarti tidak mempunyai titik potong dengan sumbu X.

Titik potong dengan sumbu Y didapatkan dengan cara mencari nilai y pada fungsi kuadrat apabila nilai peubah x sama dengan nol, sehingga akan didapatkan titik (0,y1).

Titik Ekstrim

Titik ekstrim pada fungsi kuadrat adalah sebuah koordinat dengan absisnya merupakan nilai sumbu simetri serta ordinatnya adalah nilai ekstrim.

Pasangan koordinat titik ekstrim pada fungsi kuadrat y=ax2+bx+c yaitu seperti berikut ini.

D merupakan diskriminan

D=b2-4ac

Seperti yang telah kita sebutkan di atas,

  merupakan sumbu simetri dan  adalah nilai ekstrim dari fungsi kuadrat.

Pembuktian Rumus Titik Ekstrim Fungsi Kuadrat

Titik ekstrim dapat kita peroleh dari konsep turunan pertama.

Titik ekstrim fungsi kuadrat y=ax2 + bx + c didapatkan dengan cara menurunkannya terlebih dahulu, lalu hasil turunannya sama dengan nol, y’ = 0, sehingga akan didapatkan bentuk seperti di bawah ini:

Berikut adalah tahapan untuk menggambar grafik fungsi kuadrat y=ax2+bx+c

1. Menentukan titik potong dengan sumbu koordinat.
   • Titik potong dengan sumbu X apabila y=0.
     (tidak ada untuk fungsi kuadrat yang mempunyai D<0).
   • Titik Potong dengan sumbu Y apabila x=0.
2. Tentukan titik ekstrim, yakni

Contoh soal:

Mari kita bedah bersama fungsi kuadrat dari f(x)=x2-6x+8

Titik potong dengan sumbu X 

Ingat titik potong dengan sumbu X akan didapatkan apabila nilai y=0, maka dari itu akan didapatkan bentuk persamaan kuadrat x2-6x+8=0.

Untuk memastikan bahwa persamaan kuadrat di atas mempunyai akar, maka langkah pertama adalah menentukan terlebih dahulu diskriminannya.

D=b2-4ac=(-6)2-4(1)(8)=36-32=4

Sebab diskriminannya 4 (positif) pastilah persamaan kuadratnya mempunyai dua akar real berbeda.

Hal itu berarti, fungsi kuadrat di atas mempunyai dua titik potong dengan sumbu X. Titik potong dengan sumbu X didapatkan dari akar-akar persamaan kuadrat.

x2-6x+8=0
(x-2)(x-4)=0
x=2 atau x=4

Sehingga, titik potong dengan sumbu X yaitu (2,0) dan (4,0)

Titik Potong dengan Sumbu Y 

Titik potong dengan sumbu Y akan didapatkan apabila nilai x=0.
y=x2-6x+8
y=02-6(0)+8=8

Sehinga, titik potong dengan sumbu Y yaitu (0,8)

Titik Ekstrim 

Titik ekstrim fungsi kuadrat f(x)=ax2+bx+c yaitu

Artinya untuk fungsi kuadrat f(x)=x2-6x+8 titik ekstrimnya ialah seperti di bawah ini:

Sumbu simetrinya yaitu x=3 dan nilai ekstrimnya yakni -1.

Dari informasi titik potong dengan sumbu X, titik potong dengan sumbu Y, dan juga titik ekstrim dapat kita gambar grafik fungsi kuadratnya.

Tahapannya, sesudah mendapatkan titik potong dengan sumbu X, titik potong dengan sumbu Y, dan juga titik ekstrim. Lalu gambarkan titik-titik itu pada koordinat kartesius kemudian hubungkan dengan kurva halus.

Pada contoh soal di atas, fungsi kuadrat f(x)=x2-6x+8 mempunyai titik potong dengan sumbu X (2,0) dan (4,0), titik potong dengan sumbu Y (0,8) serta titik ekstrim (3,-1).

Gambar dari titik-titik ini pada koordinat kartesius ada pada gambar di bawah ini.

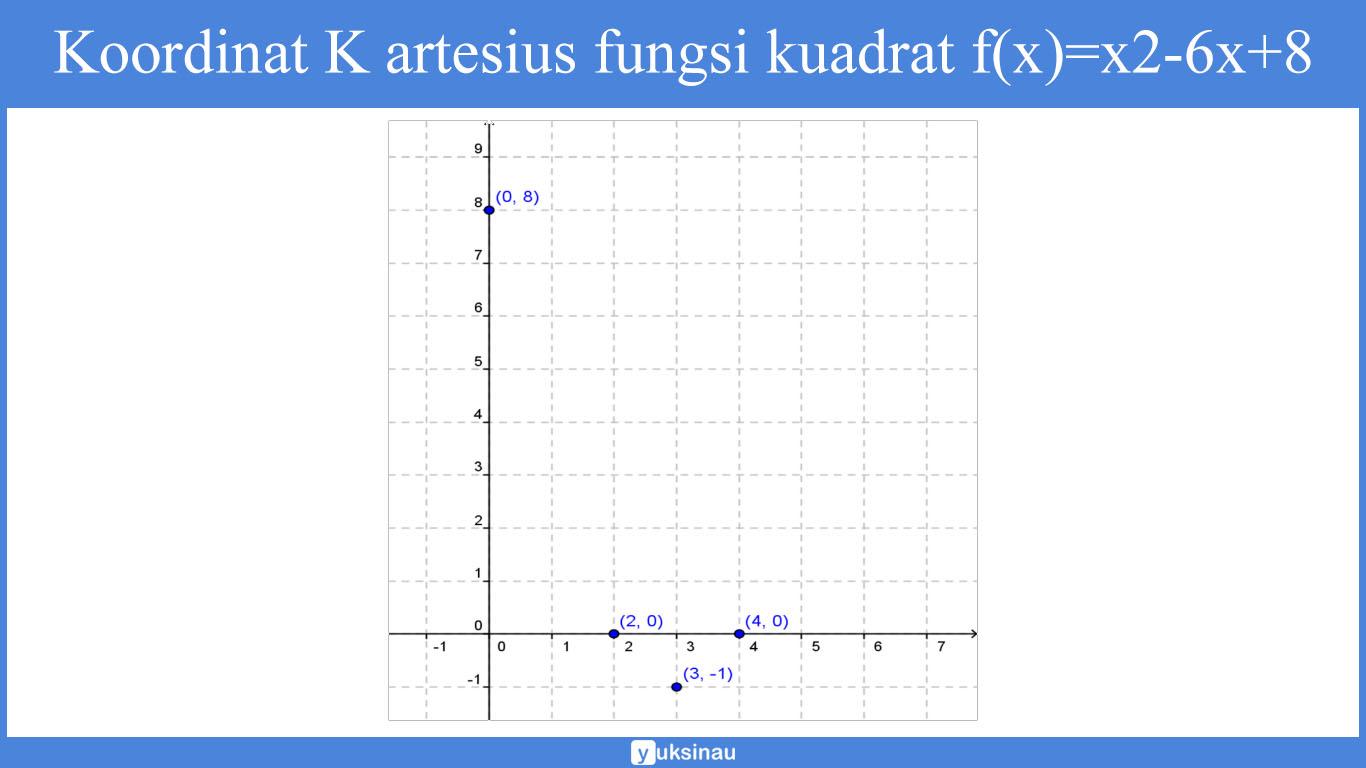
Kemudian hubungkan titik-titik tersebut dengan satu kurva halus, sehingga akan didapatkan kurva fungsi kuadrat f(x)=x2-6x+8 seperti berikut ini:

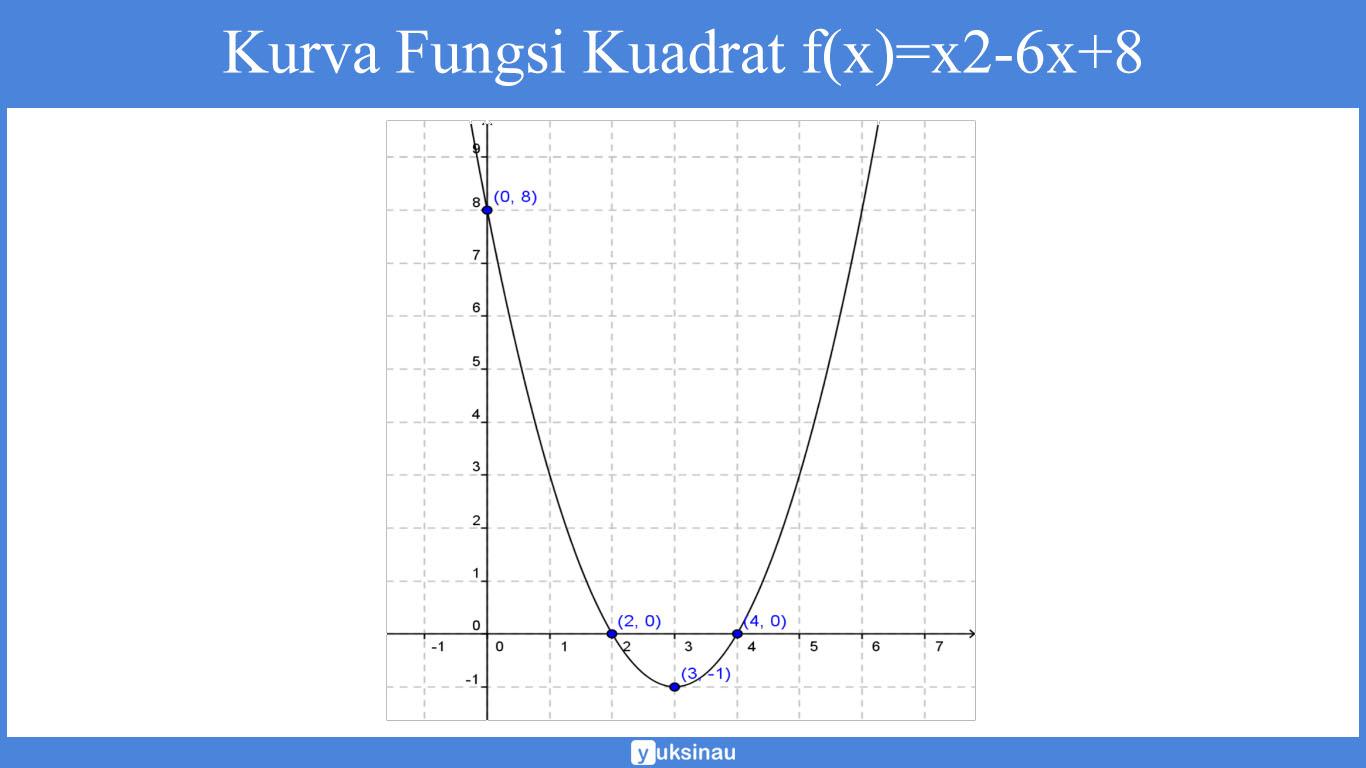
Sifat Kurva Parabola

1. Berdasarkan koefisien “ɑ”

Nilai a memiliki fungsi sebagai penentu arah membukanya suatu grafik.

• Apabila a > 0, parabola terbuka ke atas sementara titik baliknya minimum sehingga memiliki nilai minimum.
• Apabila a < 0, parabola terbuka ke bawah sementara titik baliknya maksimum sehingga memiliki nilai maksimum.

2. Berdasarkan koefisien “b”

Nilai b memiliki fungsi sebagai penentu untuk menentukan posisi sumbu simetri yang ada pada grafik.

• Untuk a dan b bertanda sama (a > 0, b > 0) atau (a < 0, b <0) maka, sumbu simetri posisinya ada di kiri sumbu y.
• Untuk a dan b berlainan tanda (a < 0, b > 0) atau (a > 0, b < 0) maka, sumbu simetri posisinya ada di kanan sumbu y.

3. Berdasarkan koefisien “c”

Nilai c memiliki fungsi sebagai penentu titik potong dengan sumbu y.

• Apabila c > 0, grafik parabola memotong di sumbu y positif.
• Apabila c < 0, grafik parabola memotong di sumbu y negatif.

4. Berdasarkan D = b2 – 4ac (diskriminan)

• Apabila D > 0 persamaan kuadrat memiliki dua akar real yang berlainan.
  Parabola akan memotong sumbu x di dua titik. Untuk D kuadrat sempurna maka kedua akarnya rasional, sementara D tidak berbentuk kuadrat sempurna maka kedua akarnya berupa akar irasional.
• Apabila D = 0 persamaan kuadrat memiliki dua akar yang sama (akar kembar), real, dan juga rasional. Parabola akan menyinggung pada sumbu x.
• Apabila D < 0 persamaan kuadrat tidak memiliki akar real atau kedua akarnya tidak real (imajiner). Parabola tidak akan memotong serta tidak akan menyinggung di sumbu x.
  • Untuk D < 0, a > 0 parabola akan selalu berada di atas sumbu x atau biasa disebut sebagai definit positif.
  • Untuk D < 0, ɑ < 0 parabola akan selalu berada di bawah sumbu x atau biasa disebut sebagai definit negatif.

Menyusun Fungsi kuadrat

1. Jika memotong pada sumbu x di (x1,0) dan (x2,0), maka rumus yang berlaku yaitu: y = ƒ (x) = ɑ (x – x1) (x – x2).
2. Jika titik puncak (xp, yp) maka rumus yang berlaku yaitu: y = ƒ (x) = ɑ (x – xp)2 + yp.
3. Jika menyinggung sumbu x di (x1,0) maka rumus yang berlaku yaitu: y = ƒ (x) = ɑ (x – x1)2

Hubungan Garis Dengan Parabola

Berdasarkan D = b2 – 4ac, kedudukan garis pada parabola dibagi menjadi 3 macam, antara lain:

1. D > 0 berarti garis akan memotong parabola ada di dua titik.
2. D = 0 berarti garis memotong parabola di satu titik (menyinggung)
3. D < 0 berarti garis tidak memotong dan tidak akan menyinggung parabola.

Contoh Soal dan Pembahasan

Soal 1:

Apabila fungsi f(x)=px2-(p+1)x-6 mencapai nilai tertinggi untuk x=-1, maka tentukan nilai p.

Jawab:

x=-1 merupakan sumbu simetri, rumusnya -b/2a.

Artinya: -b/2a=-1
-(-(p+1))/2(p)=-1
p+1=-2p
3p=-1
p=-1/3

Soal 2: 

Menentukan titik ekstrim dan juga titik potong dengan sumbu X untuk fungsi kuadrat
f(x)=x2-20x+75.

Jawab:
Titik ekstrim rumusnya:

Titik potong dengan sumbu X apabila y=0 untuk fungsi kuadrat y=x2-20x+75 titik ekstrimnya:

Titik potong dengan sumbu X

x2-20x+75=0
(x-5)(x-15)=0
x=5 atau x=15 sehingga titik potongnya adalah (5,0) dan (15,0)

Soal 3:
Koordinat titik balik grafik fungsi kuadrat y=x2+4x-6 yaitu…

Jawab:

Koordinat balik rumusnya yaitu:

Soal 4: 

Diketahui f(x) = -x2 + 5x + c, apbila ordinat puncaknya 6 maka nilai c yaitu…

Jawab:

Ordinat titik puncak, rumus: -D/4a
-(52-4(-1)c)/4(-1) = 6
-(25+4c)/-4=6
-(25+4c)=-24
25+4c=24
4c=-1
c=-1/4

Selanjutnya akan kami berikan contoh soal pada SNMPTN dan juga UN mengenai fungsi kuadrat, simak baik-baik pembahasan di bawah ini:

Soal 1. (MADAS SNMPTN 2012)

Jika gambar di bawah ini adalah grafik fungsi kuadrat f dengan titik puncak (-2,0) dan melalui titik (0,-4) maka nilai f(-5) adalah …

1. -7
2. -8
3. -9
4. -10
5. -11

Jawab:

Diketahui titik puncak ( xp , yp) = (-2,0), melewati titik (x , y) = (0,-4)

Rumus yang sesuai jika diketahui titik puncaknya adalah:

y = f(x) = a(x-xp )2 + yp

Untuk mencari nilai a, maka:

y = f(x) = a(x-xp)2 + yp
y = a(x+2)2 + 0
-4 = a(0+2)2 + 0
-4 = 4a
a = -1

Sehingga akan diperoleh:
f(x) = -(x + 2)2, dengan f(-5)
f(-5) = -(-5 + 2)2 = -9

Jadi, jawabannya yaitu: C

Soal 2. (MatDas SBMPTN 2013)

Jika grafik fungsi kuadrat f(x) = ax2 + bx + c mempunyai titik puncak (8,4) dan memotong sumbu-x negatif maka …

1. a > 0, b > 0 dan c > 0
2. a < 0, b < 0 dan c > 0
3. a < 0, b > 0 dan c < 0
4. a > 0, b > 0 dan c < 0
5. a < 0, b > 0 dan c > 0

Jawab:

Diketahui titik puncaknya adalah (8,4), sehingga grafik terbuka ke bawah, maka:

a < 0
xp = -b/2a = 8, karena a < 0 → b > 0
D = b2 – 4ac, syarat memotong sumbu x negatif D > 0 sebab b > 0 dan a < 0, maka:
b2 – 4ac > 0
(+) – 4(-)c > 0
c > 0

Jadi jawabannya yaitu: E

Soal 3. (Matematika IPA SBMPTN 2014)

Diketahui suatu parabola simetris terhadap garis x = -2 dan garis singgung parabola tersebut dititik (0,1) sejajar dengan garis 4x + y = 4 . Titik puncak parabola tersebut adalah …

1. (-2,-3)
2. (-2,-2)
3. (-2,0)
4. (-2,1)
5. (-2,5)

Jawab: 

Misalkan persamaan parabolanya adalah  y = ax2 + bx + c parabola simetris kepada garis xp = -2 maka tentukan xp = -b/2a =-2 → b = 4

garis ≡ 4x+y = 4 → mg = -4
Sebab sejajar  maka mparabola = mgaris = -4
mparabola = y
2ax + b = -4 lewat titik (0,1)
2a(0) + b = -4
b = -4

Untuk menentukan xp dan yp:
b = 4a
-4 = 4a
a = -1

Persamaan parabola y = ax2 + bx + c adala:h sebagai berikut
y = -x2 – 4x + c melalui titik (0,1)
1 = -02 – 4(0) + c
c = 1

Maka bisa dihitung y = -x2 – 4x + 1
xp = -b/2a = -(-4)/2(-1) = -2 dan yp = -(-2)2 – 4(-2) +1= 5

Sehingga titik puncak parabolanya yaitu (-2,5)

Jadi jawabannya yaitu: E

Soal 4. (UN 2008)

Persamaan grafik fungsi kuadrat yang melalui titik A(1,0), B(3,0), dan C(0,-6) adalah …

1. y = 2x2 + 8x – 6
2. y = -2x2 + 8x – 6
3. y = 2x2 – 8x + 6
4. y = -2x2 – 8x – 6
5. y = -x2  + 4x – 6

Jawab:

Untuk titik C (0,-6) → x = 0, y = – 6

Untuk titik A (1,0) dan B (3,0) → x1 = 1, x2 = 3

Maka rumus yang berlaku adalah y = a(x – x1)(x – x2)

y = a(x – 1)(x – 3)
– 6 = (0 – 1)(0 – 3)
– 6 = 3a
a = – 2

Menentukan fungsi kuadrat caranya:

y = a(x – x1)(x – x2)
y = – 2(x – 1)(x – 3)
y = – 2(x2 – 4x + 3)
y = – 2x2 + 8x – 6

Jadi jawabannya yaitu: B

Soal 5. (UN 2007)

Perhatikan gambar!

Persamaan grafik fungsi kuadrat pada gambar adalah …

1. y = -2x2 + 4x + 3
2. y = -2x2 + 4x + 2
3. y = -x2 + 2x + 3
4. y = -2x2 + 4x – 6
5. y = -x2 + 2x – 5

Jawab:

Diketahui:
(xp , yp) = (1,4)
(x , y)  = (0,3)

Ditanyakan: fungsi kuadrat yang akan terbentuk?

Untuk parabola yang mempunyai titik puncak rumus yang berlaku seperti di bawah ini:
y = a(x – xp)2 + yp
y = a (x – 1)2 + 4
3 = a(0 -1)2 + 4
3 = a + 4
a = -1

Fungsi kuadrat yang terbentuk yaitu:
y = a(x – xp)2 + yp
y = -1(x -1)2 + 4
y = -x2 + 2x + 3

Jadi jawabannya yaitu: C

Demikianlah ulasan singkat terkait Fungsi Kuadrat yang dapat kami sampaikan. Semoga ulasan di atas mengenai fungsi kuadrat dapat kalian jadikan sebagai bahan belajar kalian.

sumber: https://www.yuksinau.id/fungsi-kuadrat/